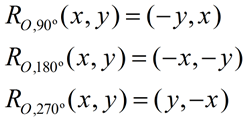|
For a review of rotations, see the Refresher section Transformations: Rotations.
Now let's expand that knowledge of rotations in relation to geometry.
Intuitively, a rotation turns a figure through an angle about a fixed point called the center.
 |
A rotation is a rigid transformation (isometry) where if center P is a fixed point in the plane, θ is the angle of rotation, and point A ≠ P, then
RP,θ (A) = A' and m∠APA' = θ. If A = P then RP,θ (P) = P. |
|
So what is this definition saying??
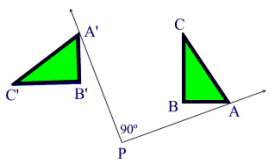
Part I (first sentence): At the right is an example where the center of rotation is fixed point P, and the angle of rotation (θ) is 90 degrees. The point A is not the same as point P. The 90º rotation of A about P will yield A'. The m∠ APA' = 90º. Notation: RP,90º ( A) = A'
Part II (second sentence):
"If A = P then RP,θ (P) = P." If A and P are the same point, you are trying to rotate a point about itself. There will be no visible change in such a rotation. The rotation equals itself:
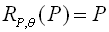
|
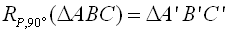
rotation counterclockwise
|
"A rotation requires knowing the center (point) and the measure (direction)
of the angle of rotation." NGMS

 Remember, that in a rotation, the points A, B and C in a triangle (for example),
will always retain their same distances from the center point of rotation.
As seen in the diagram below, each point follows an "arc path" during a rotation.
(The dashed "circular arc paths" in the diagram below represent the circles, with center P,
through each of the triangle's vertices.
Note that PC=PC', for example, since they are the radii of the same circle.)
|
In this rotation that maps ΔABC to ΔA'B'C', each point and its corresponding image are the same distances from the
center of rotation, P.
Note the circular arc through A and A', B and B', and C and C'. This shows that:
AP = A'P BP = B'P CP = C'P
Unlike reflections and translations, the segments connecting pre-image and image points are NOT parallel.
|
Orientation (lettering): The lettering of the points of the pre-image, in this diagram, is counterclockwise A-B-C, and the image is also lettered counterclockwise A'-B'-C'.
|
|
Properties preserved under a rotation from the pre-image to the image.
1. distance (lengths of segments remain the same)
2. angle measures (remain the same)
3. parallelism (parallel lines remain parallel)
4. collinearity (points remain on the same lines)
5. orientation (lettering order remains the same)
|
|
|

A positive angle of rotation turns a figure counterclockwise (CCW),
and a negative angle of rotation turns the figure clockwise, (CW).
There are two possible directions to travel when rotating.
Look at point P in the diagram at the right. The positive x-axis is considered the "starting" location of 0º. You can have an angle of rotation of positive 135º counterclockwise to point P, or a negative angle of 225º clockwise to point P.
Notice that together, the angles (135º and 225º) form a complete circle (360º).
It is even possible to have one complete revolution (360º) PLUS an additional 135º to get to P (an angle of rotation of 495º). |
|
When working in the coordinate plane, it is important to have a visual understanding of how the quadrants are divided through rotational angles.
The most common angles seen on the grid are multiples of 15º. The "favorite" angles are usually 30º, 45º, 60º, 90º, 135º, 180º, and 270º. |
|


Let's take a closer look at how the basic mapping rules apply geometrically.
Remember, these formulas are counterclockwise rotations centered at the origin.
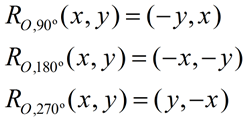
| Rotating the point R(5,2) 90º CCW About the Origin: |
|
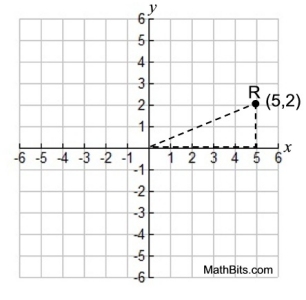 |
• Plot the point R(5,2).
• Sketch a right triangle as shown.
• Think about using tracing paper to make a copy of the triangle.

• Remember that the x-axis and y-axis are perpendicular to one another, forming 90º angles seen in each Quadrant. |
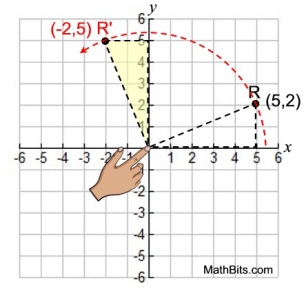 |
With the traced triangle copy on top of the original triangle...
•
Hold your finger on the traced triangle at the center of the rotation (the origin).
• Rotate the traced triangle 90º CCW.
• Observe the coordinates of R' at (-2,5).
• A rotation of 90º CCW centered at the origin
maps (x,y) to (-y,x).
|
The same procedure, as shown above, can be used for a 180º rotation and a 270º rotation.
Rotating the point R(5,2)
180º CCW About the Origin: |
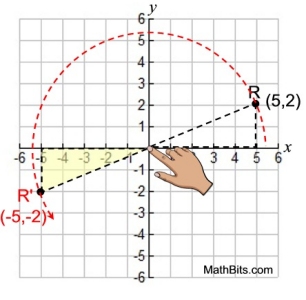
• A rotation of 180º CCW centered
at the origin
maps (x,y) to (-x,-y). |
Rotating the point R(5,2)
270º CCW About the Origin: |
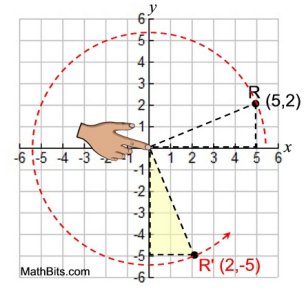
• A rotation of 270º CCW centered
at the origin
maps (x,y) to (y,-x). |
|
For calculator
help with
transformations
ROTATIONS
click here.
|
|

NOTE: The re-posting of materials (in part or whole) from this site to the Internet
is copyright violation
and is not considered "fair use" for educators. Please read the "Terms of Use". |
|